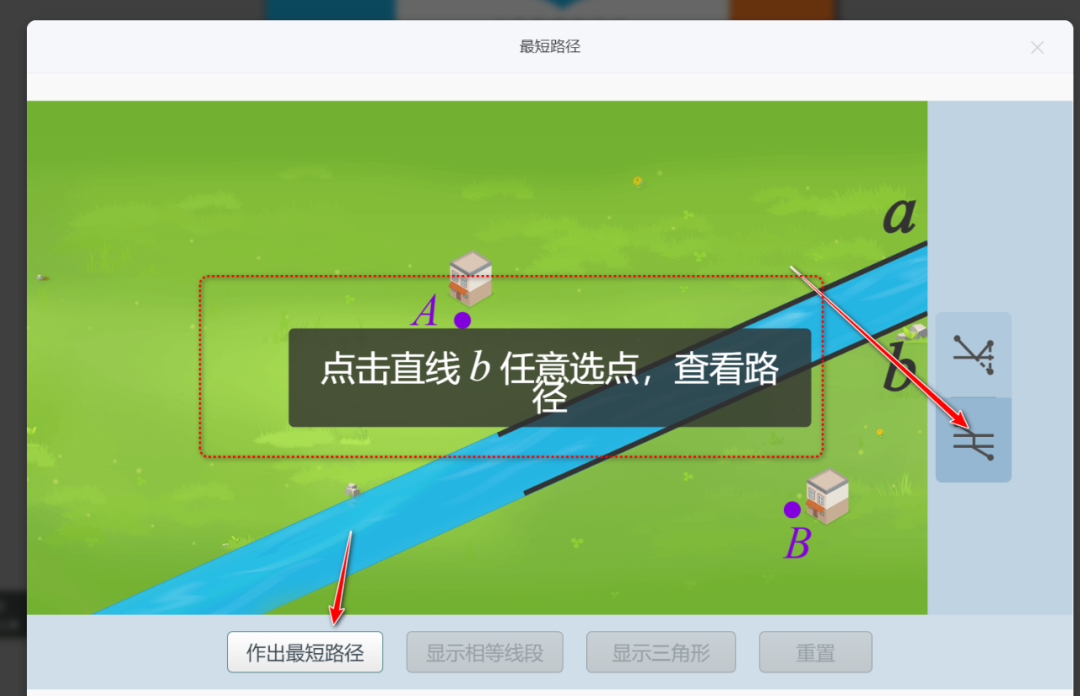
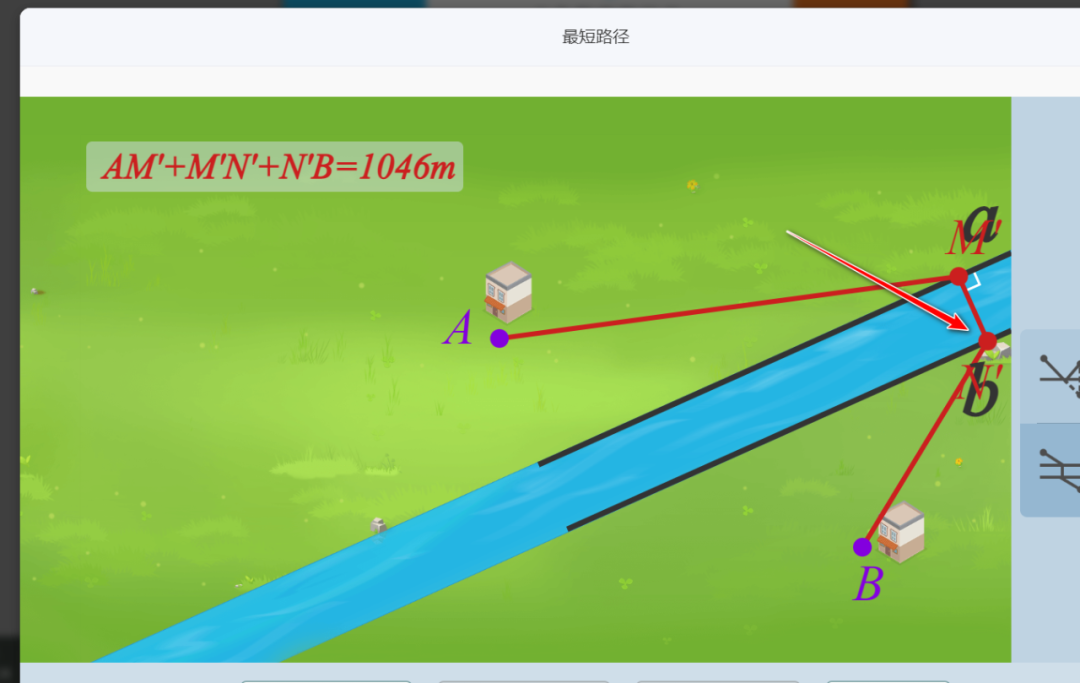
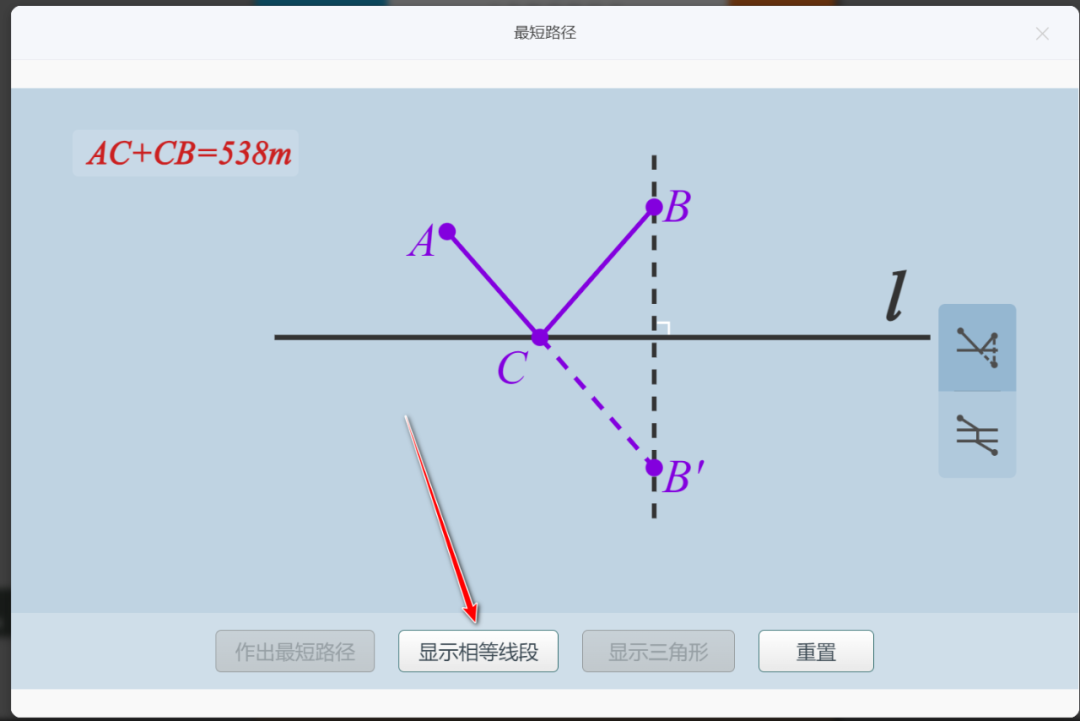
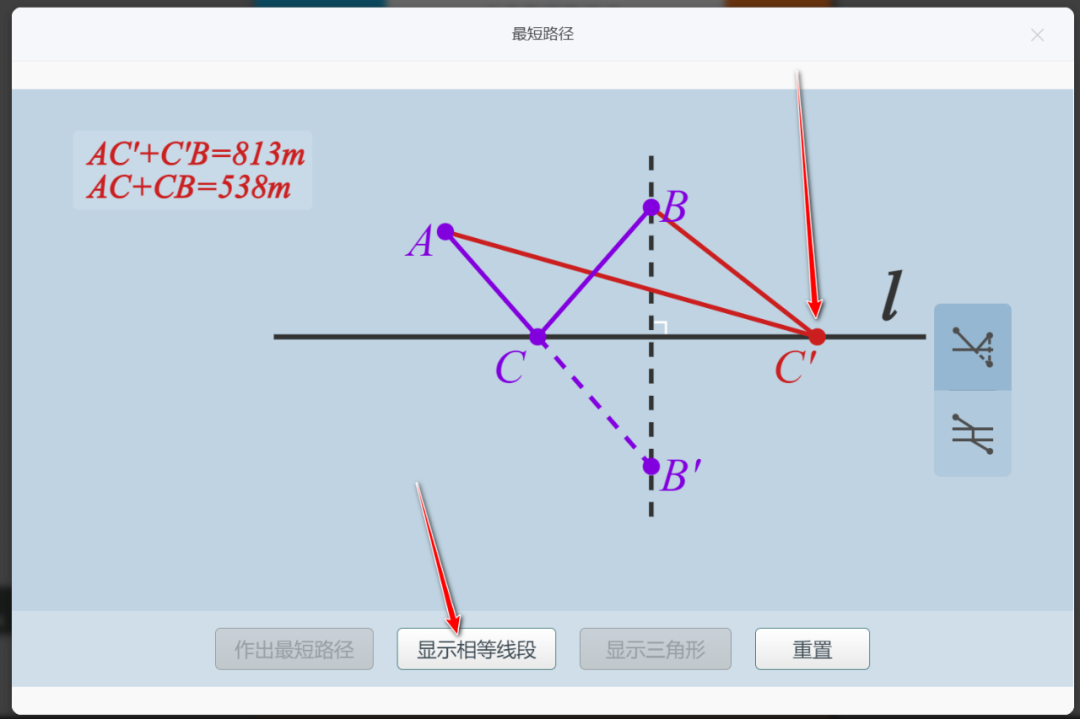
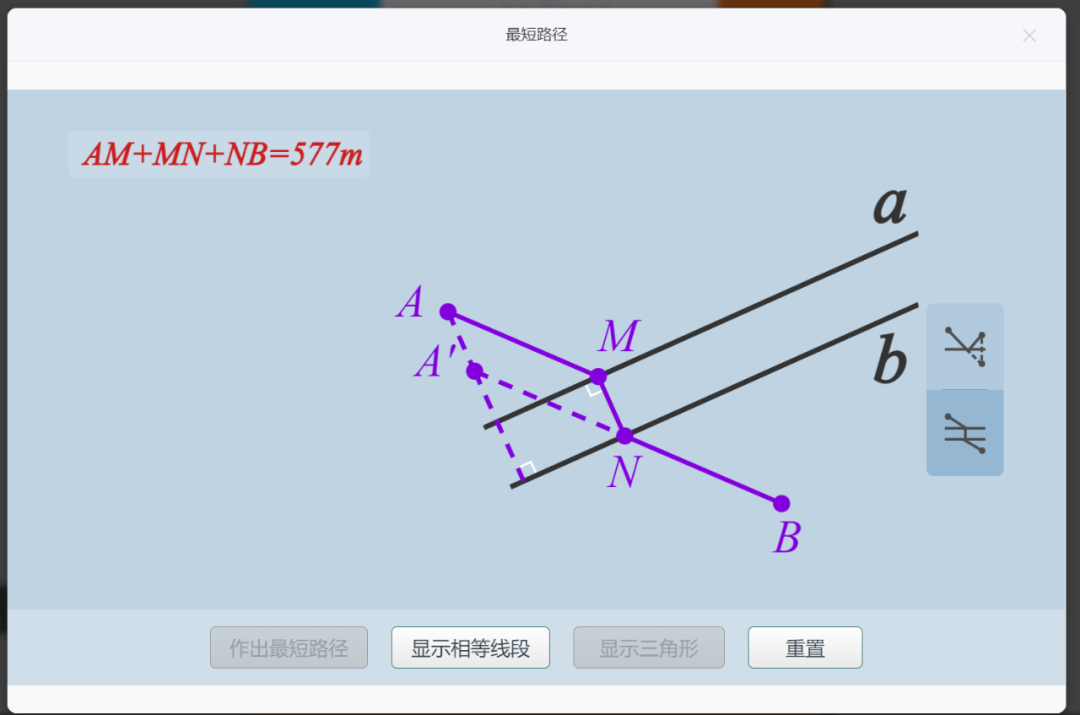
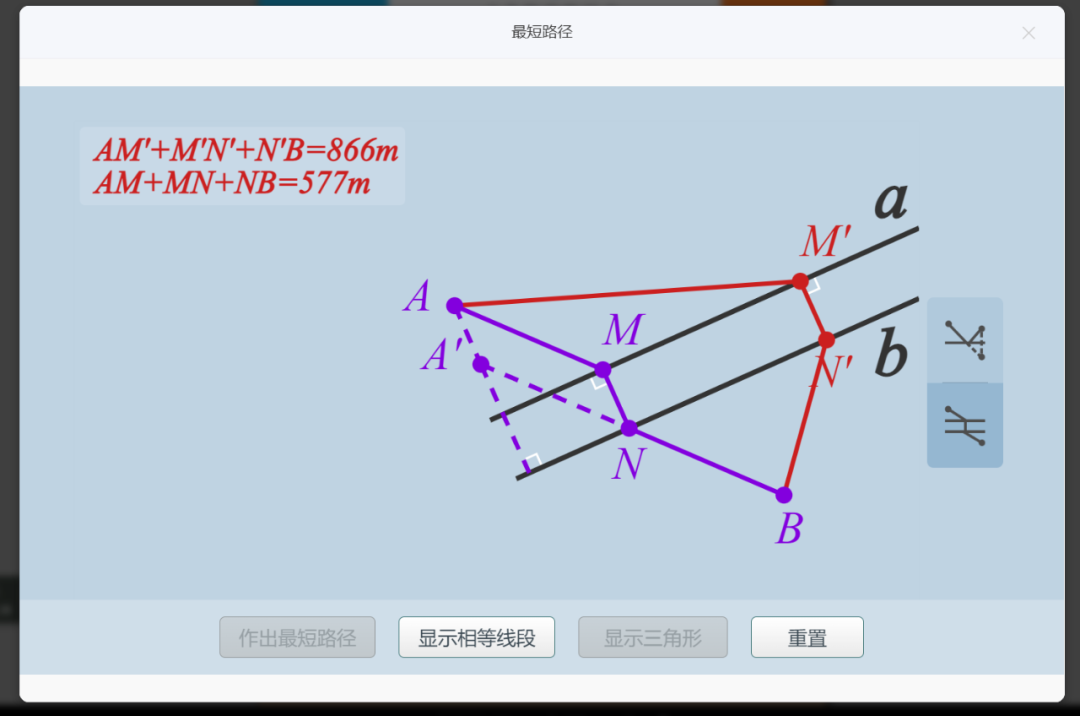
以下是有关这个主题在中小学缴费中的一些编排和教学要求。后文笔者介绍国家智慧平台中“最短路径”工具的应用
以下是有关这个主题在中小学缴费中的一些编排和教学要求。后文笔者介绍国家智慧平台中“最短路径”工具的应用


 可以即时打开应用
可以即时打开应用


 小学阶段:直观感知与简单应用
小学阶段:直观感知与简单应用
-
基本概念(生活化场景)
-
在方格纸上寻找从A到B的最短路线(只能沿网格线走)。
-
蚂蚁爬行问题(如长方体外表面最短路径,需展开立体图形为平面)。
-
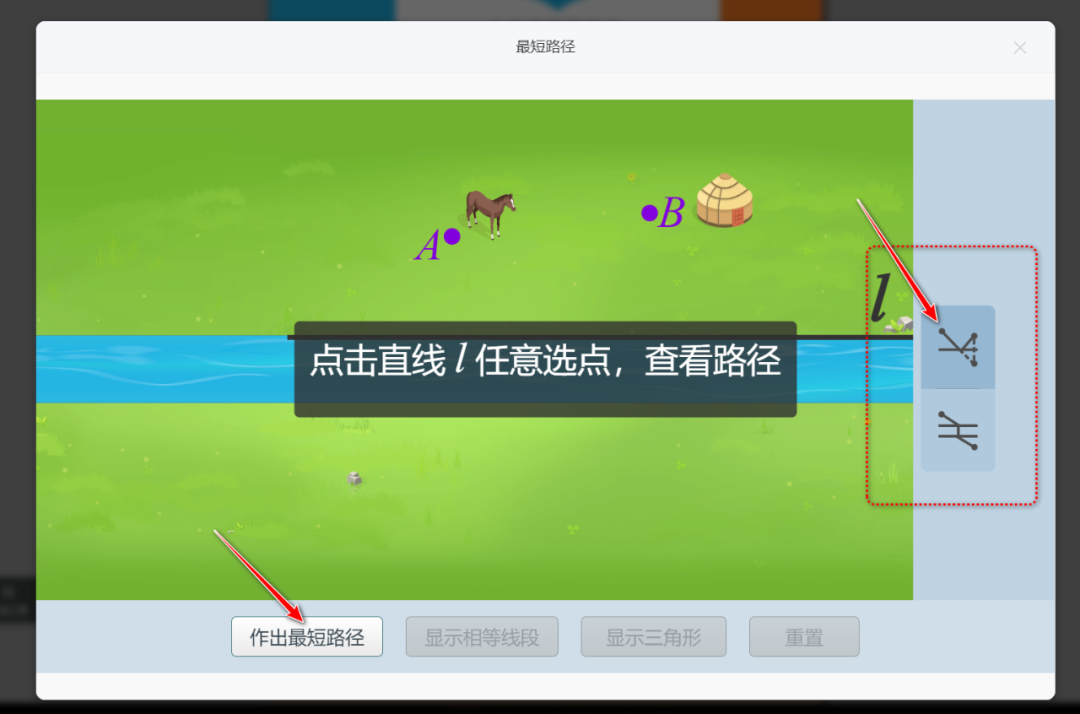
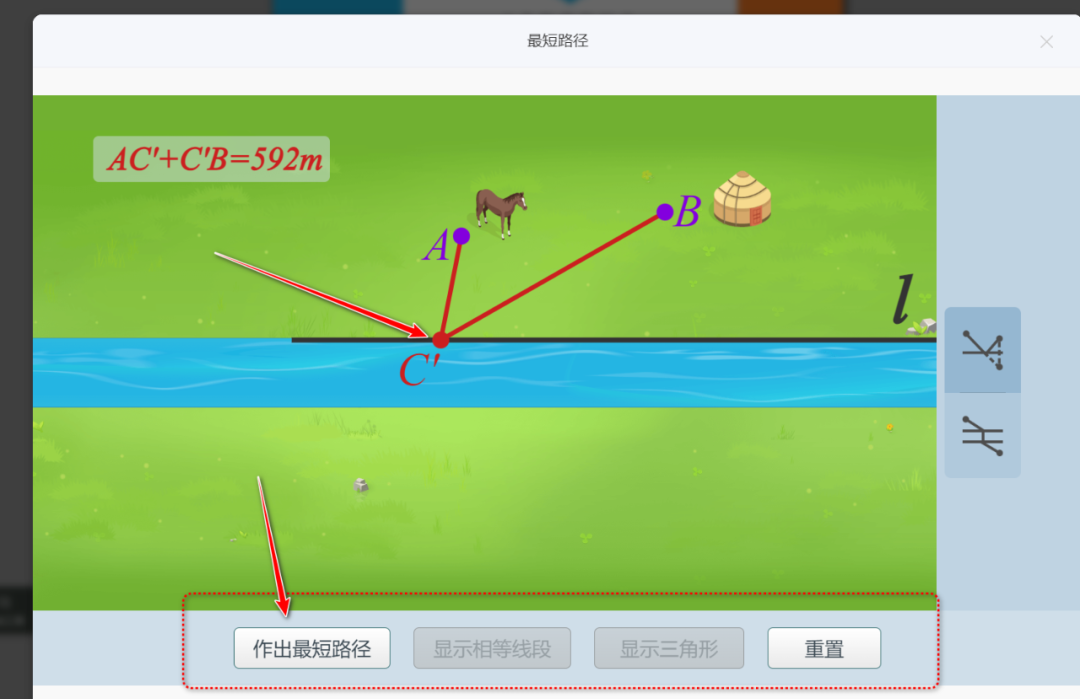
两点之间线段最短:通过生活实例(如小狗喝水问题、选择最近路线)直观理解“直线距离最短”的公理。
-
简单折线路径优化:
-
典型题型
-
“造桥选址”问题:在平行线间确定一条垂直线段使路径最短(如人教版四年级)。
-
轴对称转化法:利用对称将折线转化为直线(如将军饮马问题的最简形式)。


 初中阶段:几何模型与代数方法
初中阶段:几何模型与代数方法
-
核心模型与公理
-
“两点之间线段最短”(七年级):几何基本公理的直接应用。
-
“垂线段最短”(七年级):点到直线的最短距离。
-
经典几何模型
-
类型1:同侧两点 → 作对称点 → 连线求直线路径(八年级轴对称)。
-
类型2:两定一动(点在直线上)→ 转化为两点间线段最短。
-
拓展:两动一定(如定长线段平移问题)。
-
将军饮马问题(轴对称转化):
-
蚂蚁爬圆柱/圆锥:展开立体图形,利用勾股定理计算斜边最短(九年级投影与视图)。
-
代数方法
-
坐标系中利用勾股定理计算两点距离(八年级)。
-
结合一次函数求动态路径最小值(八年级)。


 高中阶段:图论与算法
高中阶段:图论与算法
-
图论基础(选择性必修)
-
Dijkstra算法:单源非负权图的最短路径(必修一《函数与算法》或信息技术教材)。
-
Floyd算法:多源最短路径(部分选修教材)。
-
图的基本概念:顶点、边、权重、路径。
-
最短路径算法:
-
实际应用
-
交通网络优化(地铁换乘、快递路线)。
-
通信网络布线问题。
-
跨学科渗透
-
物理:光在介质中的最短时间路径(费马原理)。
-
信息技术:编程实现Dijkstra算法(Python/C++)。
典型教材分布
| 学段 | 教材章节 | 核心内容 |
|---|---|---|
| 小学 |
|
|
| 初中 |
|
|
| 高中 |
|
|
|
|
|
|


 教学要点
教学要点
-
小学:注重动手操作(如用绳子比划)、画图实践,培养空间直觉。
-
初中:强化几何模型(对称转化)和代数工具(勾股定理)的结合。
-
高中:强调算法逻辑,通过编程实践深化理解(如用Python模拟Dijkstra)。
注:具体内容可能因教材版本(人教版、北师大版、苏教版等)和地区有所差异,但核心脉络一致:从生活直观→几何模型→算法解决,逐步提升抽象思维与应用能力。


 笔者开始介绍“最短路径”的应用方法
笔者开始介绍“最短路径”的应用方法