本期介绍数学学科工具“相遇问题”的应用。
本期介绍数学学科工具“相遇问题”的应用。
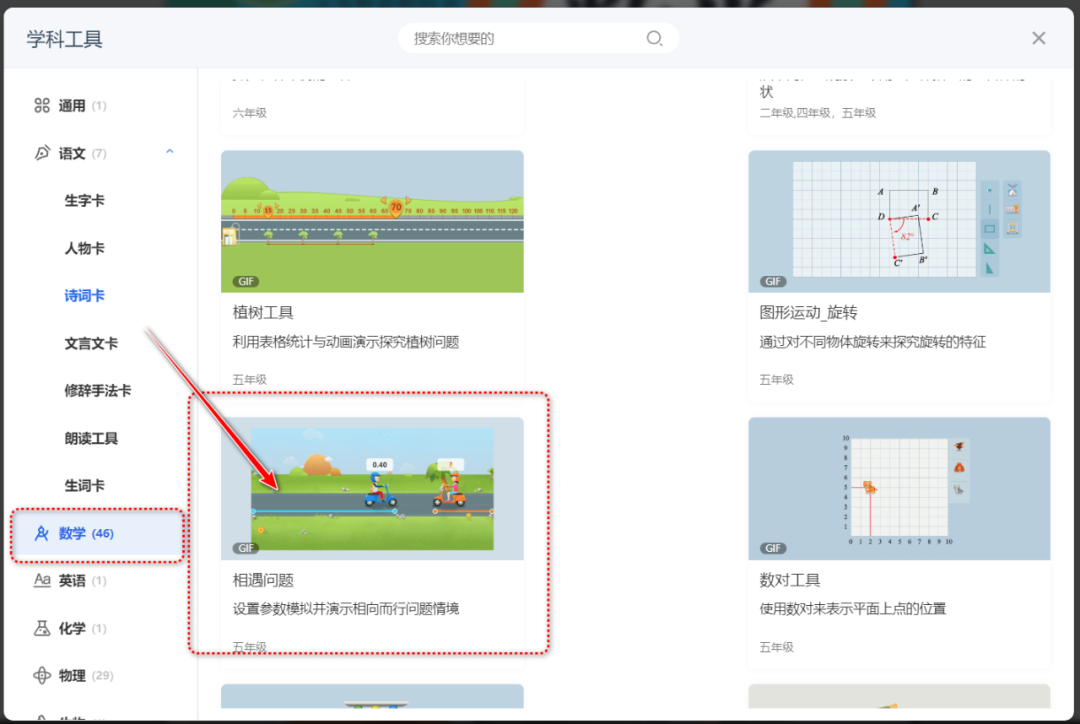

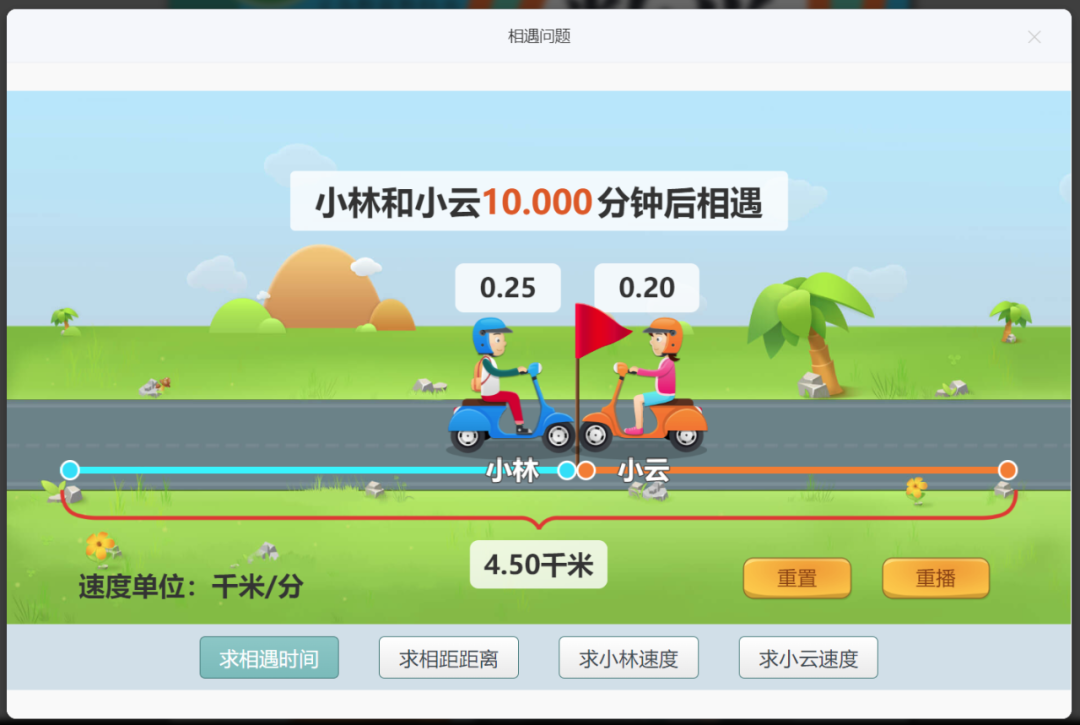
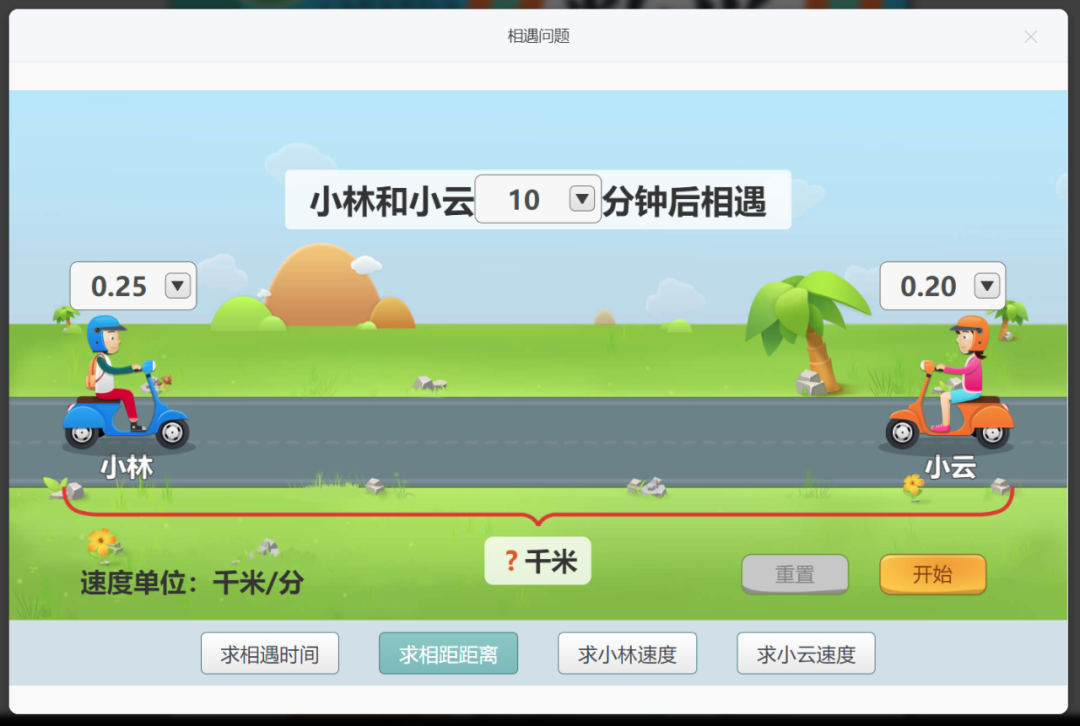
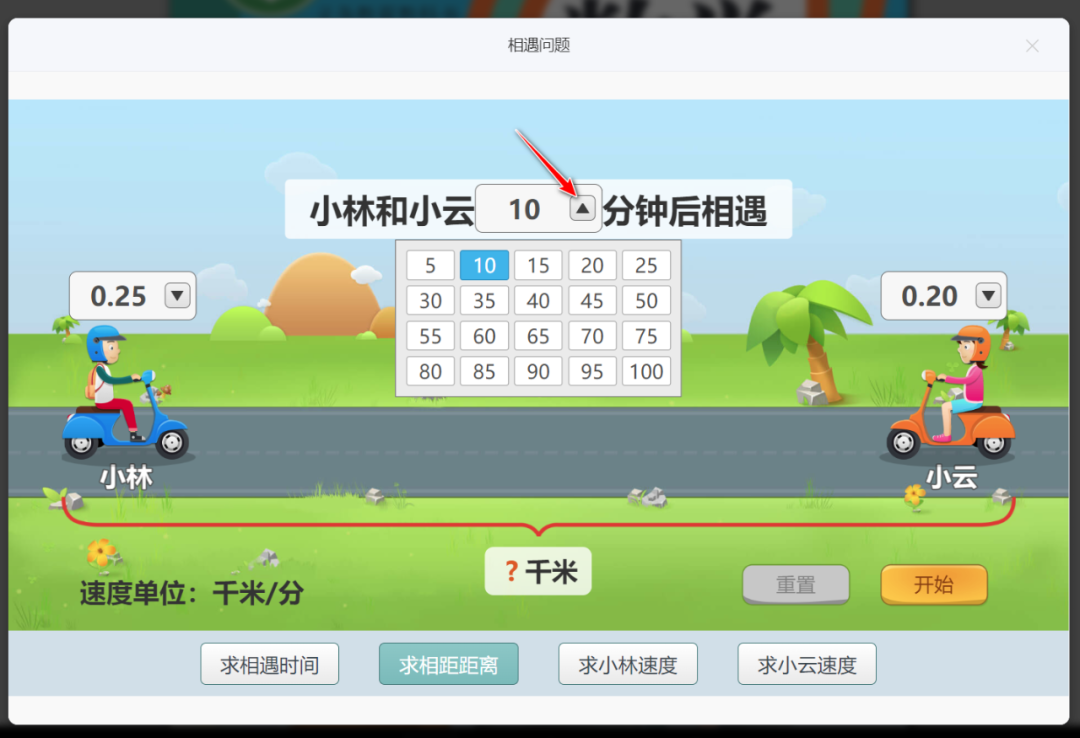
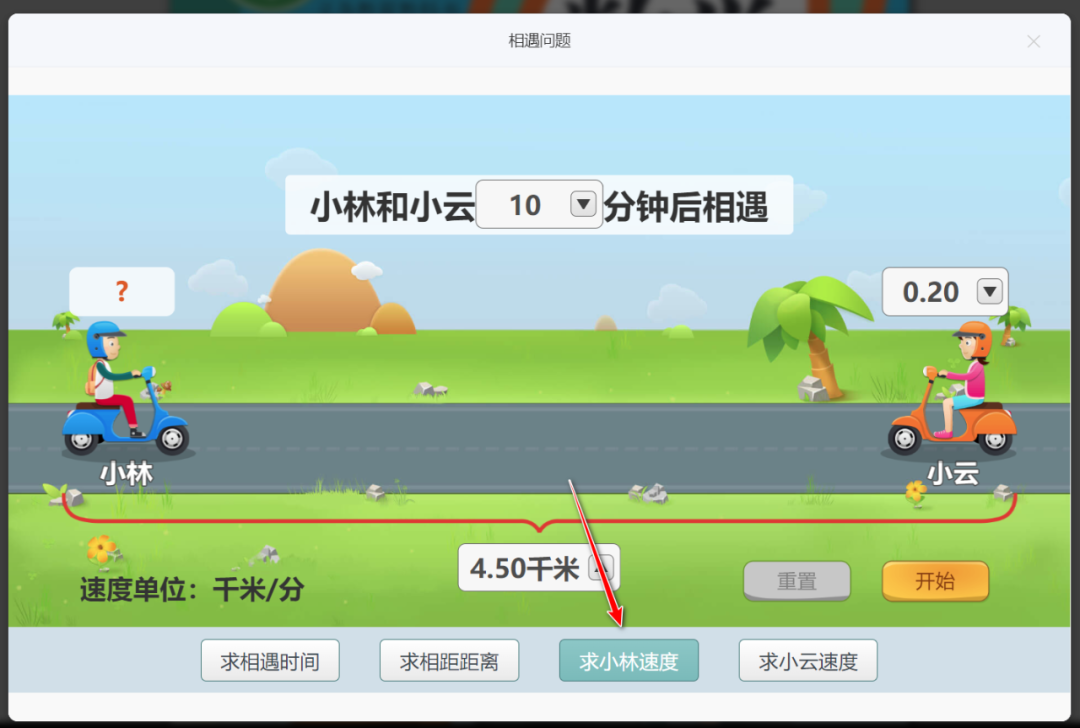
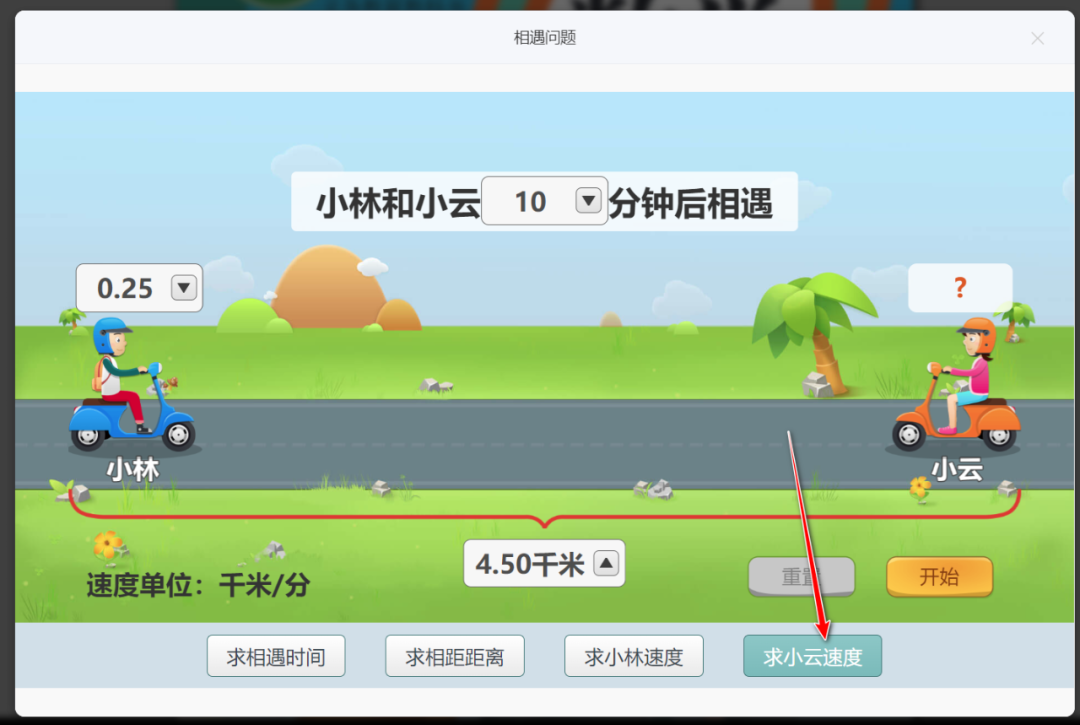



















 以下是有关小学阶段相遇问题的教材编排和教学要求。
以下是有关小学阶段相遇问题的教材编排和教学要求。一、 教材编排(一般遵循以下顺序)
-
低年级(二、三年级):铺垫与感知
-
内容:主要是简单的生活情境,如“两人从两端走向中间相遇”,侧重于直观感知“同时出发”、“相向而行”、“相遇”这些概念。计算通常涉及路程和(加法)。
-
例题:小红和小明同时从家出发去学校(学校在两家之间),小红走了60米,小明走了40米,他们相遇了。两家相距多少米?(60 + 40 = 100米)
-
重点:理解“相遇”意味着两人路程之和等于总路程。不涉及速度、时间的概念或公式。
-
中年级(三、四年级):引入速度与时间,建立基本模型
-
小明和小红同时从相距600米的两地相向而行。小明每分钟走70米,小红每分钟走50米。几分钟后他们相遇?(600 ÷ (70 + 50) = 600 ÷ 120 = 5分钟)
-
甲、乙两车同时从相距480千米的A、B两地相向开出。甲车每小时行60千米,乙车每小时行40千米。几小时后两车相遇?相遇地点离A地多远?(相遇时间:480 ÷ (60 + 40) = 4.8小时;离A地距离:60 × 4.8 = 288千米)
-
速度和 × 相遇时间 = 总路程(两地距离)
-
总路程 ÷ 速度和 = 相遇时间
-
总路程 ÷ 相遇时间 = 速度和
-
内容:明确引入“速度”和“时间”的概念。重点解决“同时出发、相向而行、相遇时所用时间相同”这一核心情形。
-
核心公式:
-
例题:
-
重点:掌握基本公式,理解“速度和”的意义,学会利用公式求相遇时间、总路程或其中一个速度。开始学习用线段图辅助分析。
-
高年级(五、六年级):变式与综合应用
-
甲车从A地开往B地,每小时行80千米。1小时后,乙车从B地开往A地,每小时行60千米。A、B两地相距600千米。乙车开出几小时后两车相遇?(设乙车开出x小时后相遇:80*(1 + x) + 60*x = 600)
-
甲、乙两人在400米环形跑道上练习跑步。两人同时从起点同向出发,甲的速度是6米/秒,乙的速度是4米/秒。他们第一次相遇需要多少秒?(相遇问题本质是追及问题:400 ÷ (6 – 4) = 200秒)注意:环形跑道上同向是追及,反向才是相遇。
-
不同时出发:一先一后出发,但相向而行直到相遇。解题关键是找到“同时运动的时间段”或利用时间差。
-
相遇地点问题:求相遇地点离某地的距离(如例题2的第二问)。
-
多次相遇:在环形跑道或两地间往返运动中的相遇问题(第一次相遇共走1个全程,第二次相遇共走3个全程,以此类推)。
-
中点相遇:相遇点在中点,意味着速度相同;相遇点不在中点,意味着速度不同。
-
综合行程问题:相遇问题与追及问题、流水行船问题等结合。
-
引入方程:用方程思想解决更复杂的相遇问题,特别是当直接套用公式困难时。
-
内容:在基本模型基础上增加复杂因素,提升分析能力和公式应用的灵活性。
-
常见变式:
-
例题:
-
重点:灵活应用基本模型分析复杂情境,掌握变式问题的解题策略,熟练运用线段图辅助分析,初步学习用方程解决行程问题。
二、 教学要求
-
理解核心概念:
-
清晰理解“同时出发”、“相向而行(相对而行)”、“相遇”、“速度和”、“总路程(两地距离)”的含义。
-
深刻理解“相遇时所用时间相同”这一关键条件。
-
理解“相遇时两人所走路程之和等于两地距离”这一基本关系。
-
掌握基本模型与公式:
-
熟练掌握“速度和 × 相遇时间 = 总路程”这一核心公式及其变形。
-
能运用公式解决标准的“同时出发、相向而行、直到相遇”的问题,求出相遇时间、总路程或其中一个速度。
-
培养分析问题能力:
-
画线段图:这是解决相遇问题(乃至所有行程问题)最重要的技能之一。教学要求学生会用线段图清晰地表示运动过程、已知量和未知量之间的关系。
-
信息提取与转化:能从题目文字描述中准确提取关键信息(速度、时间、路程、方向、是否同时出发等),并将其转化为数学模型或线段图上的元素。
-
识别问题类型:能辨别问题是标准相遇问题还是变式(如不同时出发、中点相遇等)。
-
掌握解题策略:
-
能通过调整时间或路程,将其转化为基本模型。
-
能找出实际共同运动的时间段。
-
学会用方程(设未知数)解决更复杂的关系。
-
对于基本问题,能直接应用公式求解。
-
对于变式问题(如不同时出发):
-
对于求相遇地点等问题,能结合速度比或各自的路程求解。
-
发展模型思想与数学思维:
-
体会相遇问题作为一类行程问题模型的普遍性和应用价值。
-
培养逻辑推理能力、空间想象能力(通过画图)。
-
培养解决实际问题的能力,将生活中的相遇情境抽象为数学问题。
-
计算能力:
-
能正确进行与相遇问题相关的计算(整数、小数、分数),注意单位统一(时间单位、路程单位、速度单位)。
-
能处理速度或时间涉及小数的计算。
-
解决综合问题:
-
在较高年级,能处理相遇问题与其他类型行程问题(追及、环形跑道、流水行船)或工程问题等的综合应用。
教学建议
-
重视直观演示:低年级多用实物演示、角色扮演、动画模拟等方式让学生亲身体验“同时出发”、“相向而行”、“相遇”的过程。
-
狠抓线段图:从引入相遇问题开始就严格要求学生画线段图辅助分析。教师要做好示范,引导学生掌握画图的规范和方法(标注起点、方向、速度、时间、路程、相遇点、总路程等)。
-
强调“速度和”:帮助学生理解“速度和”的意义(单位时间内两物体共同接近的距离),这是解决相遇问题的核心。
-
循序渐进,打好基础:务必让学生牢固掌握基本模型后再引入变式。基础不牢,变式问题会成为巨大障碍。
-
对比区分:将相遇问题与追及问题进行对比教学,帮助学生清晰区分“速度和”与“速度差”。
-
联系生活实际:设计贴近学生生活经验的题目,增强学习兴趣和应用意识。
-
鼓励多种解法:对于变式问题,鼓励学生尝试不同的思路(如转化法、方程法),并比较优劣。
总而言之,小学数学中的相遇问题教学,旨在引导学生从直观感知逐步过渡到抽象建模,掌握核心的数量关系(速度和×时间=总路程),并能运用这一模型(辅以线段图和灵活的策略)解决各种变式情境下的实际问题,同时培养其分析问题、解决问题和逻辑推理的能力。
以下是相遇问题核心公式的总结表格,方便理解:
| 核心公式 | 含义 | 适用情况 |
|---|---|---|
| 速度和 × 相遇时间 = 总路程 |
|
|
| 总路程 ÷ 速度和 = 相遇时间 |
|
|
| 总路程 ÷ 相遇时间 = 速度和 |
|
|
| 甲路程 + 乙路程 = 总路程 |
|
|
这个知识结构体系会帮助学生在解决相遇问题时更清晰地把握数量关系,从而更有效地解决问题。